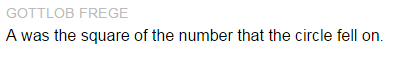Using Student Language to Drive Instruction

While I have used Desmos Polygraphs in the past, I feel as though it was only recently that I have begun to make the most of them.

Here is a summary of how the latest Polygraph I ran on Polygons played out in my classroom.

This activity was given at the beginning of the unit.  I wanted to take the informal language the students use and develop it into formal vocabulary for the unit. While the students were working, I used the dashboard not only to manage the class (making sure everyone was on task and asking appropriate questions), but to also start planning my instructional moves for after the activity. I usually just display the responses I want to share directly from the teacher dashboard, but this time I actually had time to take some screen shots and order them as slides.

I began by displaying the shapes they just saw and told them these are called polygons.

This unit will explore polygons and different characteristics or features of polygons. I asked them to think about these polygons as well as a few additional examples with counterexamples (taken from a Kagan activity) and come up with a good definition for what a polygon is.

The students did this individually before getting into groups to improve their definitions and then we shared our ideas to create a final class definition.

We talked about how this activity was meant to gather their ideas and thoughts about what features are important about polygons and how we can differentiate among all the polygons. I showed them a few questions I thought were unique and interesting in how they tried to differentiate among the polygons they had in the activity.

I feel as though this was a big moment in the lesson. Polygraphs always engage my students because of the interaction and competitiveness that takes place during the activity, but it can sometimes be challenging to maintain that engagement during the most important part of the lesson - the debrief. By starting with some fun and interesting questions I was able to hook my students back in. They are enjoying the creativity of the responses and also waiting to see if their work will be displayed and used.

Additionally, we have created a need for vocabulary. A topic that is normally dry and boring to teach has become engaging and necessary. We want to use a common language so that we can be more effective communicators and perform better in the game.  While these questions that students used were creative, they were not necessarily the most effective way to communicate about polygons. We would benefit from more precise language.

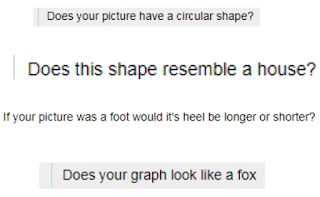
That precise language starts with the vocabulary used to classify polygons by the number of sides. It was clear that all students were already using the number of sides to differentiate the polygons. These were the first questions asked by students in the activity:

Many students used specific vocabulary indicating how many sides a polygon has and several students classified polygons further within that classification based on sides.

Specific features that differentiated those quadrilaterals were also mentioned.

At this point we took some time to record this formal vocabulary in our notes. I then moved on to show them that a lot of them focused their questions on angles and symmetry as well. We were able to do a quick review of angle vocabulary and types of symmetry based on ideas the students brought back to use.

The most powerful moment of the lesson came when sharing my favorite question.

This response came from a quiet student who would have never volunteered to share in class.  Thanks to the technology of the activity and dashboard, I was able to elicit this response from a reluctant student, collect it discreetly, and then decide to anonymously display it in front of the entire class as a model response.

I immediately praised the response in front of everyone sharing I thought this was such a unique and interesting way to phrase the question. I asked my students what they thought this person meant by “traditional?" The students correctly interpreted that “traditional” was meant to convey “equal sides and angles."

The discussion that took place allowed one student's response to be validated by the rest of the class. Instruction was not me delivering my thoughts. It consisted of students analyzing the work of other students.

I think it’s important to note the timing of the feedback I was able to give as well.  I did not have to collect papers, read through them, and then return them with written feedback.  I was doing this all within a single class period.  The technology makes it possible to review a large number of responses during class to help inform instructional decisions in real time.

We ended our class discussion exploring the idea of concave and convex polygons. I was able to show one students’ informal interpretation as well as one student who was already using the formal vocab.

These questions are a great example of how the activity allows for differentiation as a low floor/high ceiling task.  You do not need to know the formal language but it helps.

After putting together our formal definitions, we played another round or two where they could practice and put to use those formal definitions.

In using polygraphs to introduce topics, I have found it invaluable to be able to collect and use student ideas as the starting point and building blocks for developing concepts and formal definitions. The more I run polygraph activities, the better I become at sequencing the student responses during the debrief. I would love to hear other ways that teachers have used polygraphs and the teacher moves they make to get the most out of the activity.

Reflecting on using Desmos

I recently submitted a proposal to speak at NCTM on using Desmos to create opportunities for students to be right and wrong in different, interesting ways.  As I have used Desmos, this is the design principle that continues to stick out the most for me.  After seeing My Favorite No a few years back I have tried to use incorrect student responses to drive my instruction as much as possible.  Students see the teacher more interested in their thinking if they are wrong.  It validates all student thinking and encourages students to put their ideas out there.  Desmos activity builder is a tool that helps ask these types of questions.  It also easily collects, organizes, and displays student responses to help encourage whole-class discussions.

Taking the advice of Dan Meyer and Robert Kaplinsky, I proposed something that would inspire me to research it.  That research began today as I ran a Desmos activity that I created to introduce students to the equations of circles.  What follows are a few reflections on how things went.

                                     

Using Student Responses to Drive Instruction

In this activity students were to adjust sliders for different parts of the equation of a circle and observe what happens to the graph.  They would then apply what they observed to match different circles.  I also added a few error analysis questions and marble slides at the end for practice.

The first opportunity for students to be right and wrong in different, interesting ways is slide 2 where students were given the opportunity to see what part of the equation connects to the radius of the circle.  I used the variable a to represent "r^2" in the equation.   I did not want students to automatically think about the radius, and I also wanted them to notice the equation did not contain the direct value of the radius - it contains the radius squared.  I also left out the negatives for h and k because I wanted students to see the "opposite" movements.  After going over the activity, we derived the formula using the Pythagorean Theorem so that students could see why the center coordinates have the opposite sign of the values in the equation.

Below is the order in which I shared responses for slide 2 and a few notes on the discussion we had. By giving this assignment at the end of class, I was able to take my time reading the responses and organizing the progression I wanted to use in sharing them with the class.  Now that I have run this activity, I know what to look for so I would be more comfortable doing that on the fly during class.

Several students observed a change in the size and went no further. These responses speak to the accessibility of the question for all levels.  You don't need to know any math to make an observation.  It was not necessary to use any formal notation or vocabulary.  Students could just share what they saw.

The majority of students went further by identifying one of the above measurements as increasing or decreasing as the value of a increased or decreased.

There were multiple responses like the one above that mentioned the midpoint of the circle.  In my mind, this is a really interesting response.  As someone teaching geometry for the first time this year, I would not have planned to mention midpoint in a lesson on circles.  It makes perfect sense to see the center as a midpoint of the diameter of a circle though.  These students are using what they already know. Giving students the chance to play and make observations allowed me to center our class discussion on their prior knowledge and own language to develop new vocabulary.

A few students went even further and made the connection that the specific value of a was the same as the radius squared.  I found the first two responses above interesting because they did not directly say radius.  Once again, our discussion could start with those descriptions and work towards understanding exactly what they meant.  Allowing students to start the discussion created a need for a common language and vocabulary. 

Activity Design - Student Thinking

As I read through all the responses, I came across the following incorrect response on slide 16:

Once I saw this response, I went back and looked at slide 13 to find this response:

This student admits to "blindly" moving the a slider until he got the size of the circles to match.  He did not stop and notice the direct connection between the value of a and the measure of the radius.  These responses demonstrate the importance of adding slides to activities that force students to stop and explain their thinking.  Having students identify errors also encourages them to revisit previous slides to try and make connections that they might not have noticed the first time through he activity. 

Activity Design - Debriefing 

The first version of this activity had slides 16 and 17 as short answer slides.  I quickly realized that making it a multiple choice question with the option to have students explain would serve me better when debriefing the activity.  As a multiple choice question, the responses on the teacher dashboard would be organized based on the choice the student selected.  I am thankful for the design by Desmos that does not force me to choose multiple choice OR short answer.  I can easily have students select an answer from the given choices AND explain their thinking.

Reflecting on Professional Development

So this post started with me trying to answer a question posed by Dan Meyer on leading professional development: 

What is the point of opening a session on teaching and technology by asking the teachers to be students and do some math?

It has now turned into me rambling as I reflect on my experiences leading professional development sessions.

Before joining the Desmos fellowship I had only led 1 or 2 professional development sessions for teachers so my approach has evolved quite a bit over the last few months.  All of my limited experience has been leading sessions focused on Desmos. 

My number one goal used to be to give teachers something that was ready to use right away in their classrooms.  I know there were plenty of PD sessions I would attend in the past where I liked the ideas presented but would go back to my school and not have the time to implement what I took away.  I realize that goal is not realistic mainly due to two things:  time (I have yet to lead an all day session.  The sessions I have led range from 20 minutes to 90 minutes.) and the wide variety of experience/backgrounds of the teachers in any given session.  I now focus on having teachers leave with a new tool or new ideas but I understand that they most likely will not have a finished product ready to go.

My sessions then moved towards selling a tool to use in the classroom: Desmos.  I get overwhelmed trying to plan Desmos sessions because there are so many wonderful activities.  There are so many wonderful features.  There are so many subtle features that have huge impacts on teaching and learning.  I just want to show them everything!  There is no way to show everything during one session. 

It took a 20 minute session I led last week to teachers of all subjects to finally realize the most important goal of a session is to give teachers good instruction.  This is probably what the Desmos team has been telling me all along but I finally had my “Aha!” moment.  I was nervous about presenting to teachers of all subjects on a Friday after we had students for a half day.  The professional development on our half days is notorious for being a waste of time.  I knew I would have a tough crowd.  To my surprise, every session went well.  Teachers were engaged and having conversations.  My favorite moments were when we discussed feedback (When should you give it?  What should it look like? Etc…).  It was a lot of fun to listen to teachers share their perspectives across the curriculums, and all of it stemmed from a Desmos activity. 

The tool sells itself.  I don’t need to point out every little feature for them to be convinced.  They experienced an engaging lesson with great questions and wonderful opportunities to have class discussions.  I think this is why many of the Desmos fellows tend to start sessions by putting teachers in the role of students.  Teachers need to experience good instruction and see it modeled.  It doesn’t even need to necessarily be math instruction.  If they do, they will buy in and find the time to learn more about the tool you used.

As I start to plan my next session in March, the Desmos Guide to Building Great (Digital) Math Activities is where I will start and come back to throughout my presentation.  Those principles are ultimately what makes Desmos worth using.

Soft Skills

Soft skills for me includes every interaction you have with your students.  How you choose to phrase and deliver a question, correction, or request to your class as a whole or to an individual student can have a huge impact.  In some ways, I feel as though soft skills is one of my strengths.

Last week I overheard one student calling out another student for his horrible handwriting.  It was so bad that he couldn't even read it himself.  I calmly went over and mentioned how when I'm in a rush my handwriting can get pretty bad too.  One way I overcame that in school was to review my notes that night to make sure everything made sense while the material was still fresh in my head.  If I couldn't read something and figure out what it was based on the context within the notes I wrote, I could go in for help the next day.

The next day that student came to my Cav Morning (a morning study hall where students have a choice of what class to visit) having already started the homework and asked very specific and high level questions about the issues he was having with the material.  I'm not sure I can articulate how big of a deal this is.  This is a student who has not only struggled all year, but has embraced being "that student" who slacks off and just does enough to get by.  This is a class in which I have pleaded with all year to start the homework the night it is assigned instead of waiting over 24 hours to return to the new material from that class (we have block scheduling).

I believe this interaction and result shows how telling students to do something is not enough.  I have told students over and over what good study skills look like.  For this student, it didn't click until I was able to create a personal moment with him.  Instead of a lecture on what he should be doing, I made myself vulnerable by sharing my own struggles and the strategies I use to deal with those struggles.  As teachers we have to seek out those opportunities.

Another small thing I consider a soft skill is something I picked up during my student teaching.  I try to ask "Does this make sense?" instead of "Are there any questions?"  I'm not sure how much difference this makes but I like how it allows students to simply say no or even just shake their heads to keep our conversations going.  They don't have to formulate an entire question or get embarrassed by speaking up in front of everyone.  It also creates a culture where we aren't focused on the answer.  I'm not asking if students got the correct answer.  I'm asking if students understand where that answer came from.

When a student does ask a question, I make a point of praising that student.  A simple "Thanks for asking that question" or "That is a really great perspective to think about" goes a long way to encourage more questions.  I like to point out that student questions help me become a better teacher.  I share with students how they help me focus and adjust my teaching.  I also like to point out that questions show me that you are trying to make sense of the material.  You aren't just copying down information to memorize.  These small comments can help build up a safe and productive classroom environment over time.

There are other soft skills that I really have to work at though and that's why I appreciated Sam Shah's honesty in his post Not all of us have soft skills. I don't like talking about myself and usually won't do it unless prompted so it can be difficult for me to quickly form the necessary relationships with my students.  Sara Van Der Wer's post on name tents inspired me to try something similar this year.  It made a huge difference in how quickly I gained buy-in from my students.  I plan to use it again next year but spread it out over the first month of school.

Starting this calendar year I have also challenged myself to be more available and present for my students in the morning.  If I don't have any students asking me questions during our aforementioned Cav Monrning I tend to use that time to plan lessons or grade.  From now on, I will put my work aside and come out from behind my desk.  I do not want to isolate myself from my students during this time.  It's easy to get caught up with all the planning, grading, and other administrative tasks in teaching but those things will get done.  I need to prioritize taking advantage of this great opportunity to have casual conversations with my students and strengthen those relationships.

---Side note:  I'm going to continue to throw some love to Sam Shah as I highly recommend you read his recent post on Girls and Math.  It's a very timely post with the release of Hidden Figures and I felt as though I could really relate to a lot of what he had to say.  It has motivated me to try and organize either a viewing of the movie or reading of the book with my students.

My Favorite: The Desmos Guide to Building Great Math Activities

So this whole blog thing hasn't been very successful so far this school year, but thanks to the MTBoS 2017 Blogging Initiative I have reason and motivation to post throughout the month of January!  

The obvious choice for my favorite thing is Desmos.  What is not immediately as obvious is just how much Desmos influences my planning and instruction.  Its influence goes well beyond the specific graphs and activities I use in class.  Using Desmos and being part of the Desmos teaching fellowship has shifted my entire approach to planning and instruction.

The Desmos Guide to Building Great (Digital) Math Activities provides awesome recommendations for planning any math activity.  It does not matter if you are using Desmos or some other technology or no technology at all.  I have noticed myself creating lessons outside of Desmos that ask for informal before formal, create an intellectual need for new skills, give students opportunities to be right and wrong in different and interesting ways, delay feedback for reflection, and connect representations.  Many times Desmos helps me to accomplish these things more easily and more effectively but it's not a requirement.  

One of my favorite recommendations is to create an activity that is easy to start and difficult to finish.   I continue to focus on this recommendation as I look to improve my lessons.  One of the biggest challenges teachers face is the varied abilities and academic backgrounds that a single class can contain.  There are many Desmos activities that are not only great to use in the classroom but are also a great model of how to actually differentiate effectively.  Even if I don't use an activity in class, I can still take that model and apply it to a different topic or lesson that might not even use Desmos.

I have improved many of my lessons by incorporating Desmos, but I have improved an even larger amount by incorporating the recommendations made in the Desmos Guide to Building Great (Digital) Math Activities.  Desmos brings more than a tool to your classroom.  It brings a shift in your instructional approach.

Desmos PD

Today, I gave a PD session covering Desmos.  Compared to last year, I had less time (only 50 minutes) and more teachers (about 30) for my session.  I was excited to see an increase of teachers interested in learning more about Desmos.

I had a google form for teachers to fill out as they entered so I could get an idea of the experience level of the class.  I really did not know what to expect as far as how many teachers were already using Desmos.  About 50% of the teachers were not using Desmos at all.  With this in mind, I really wanted teachers to leave my session with a basic understanding of the Desmos web site set up (calculator vs activities) while being exposed to as many of the great features as possible.  I also wanted them to get both a student and teacher perspective as they start to envision how Desmos could fit into their own classroom.

After the survey, teachers jumped into an activity.  I chose "Card Sort: Linear Systems" by Michael Fenton because it demonstrates dragging a point, sketching, and card sorts.  Many of the teachers who used Desmos last year were not aware of the card sort.  I displayed the teacher screen as they worked so they could start thinking about their role as the teacher when their students would be completing an activity.

Since so many teachers were not using Desmos already, I gave them a brief history and overview after they completed the Card Sort activity.  We quickly looked at the calculator before focusing on the activities from the student perspective and then the teacher perspective.  There were some good questions and conversations about how to display student work to start class conversations.

Some teachers were looking for a way to create answer keys and grade student work quickly.  I tried to emphasize that the power of Desmos activities is that it provides students with a way to investigate and explore topics in the beginning of a lesson.  It also serves as a great formative assessment tool.  I realized where some teachers see the inability to give students instant feedback as a weakness of Desmos activities, I see it as a strength.  If a student answers a question and immediately knows whether they got it right or wrong, they are done with that problem.  Desmos activities give the teacher the opportunity to revisit the problem with the class while students are still invested in the problem.  The teacher can lead the class to a consensus by looking at all the student responses.  Students are able to confirm or correct each other's work instead of the teacher.  This set up is a much more powerful way to learn.

After sharing a few of my favorite activities and going through how to search, copy, and edit activities, I made my biggest mistake for the session.  With about 10-15 minutes left in the session, I encouraged teachers to either search and explore activities specific to their classes or try out the scavenger hunts to better familiarize themselves with Desmos.  I was going to stop them with a couple minutes left to take any remaining questions and wrap everything up.  Many of the teachers interpreted this instruction as the session was over.  They chose to take an early lunch as my session was the last one before our break.  As with many of my lessons with students, I did not have good closure for my lesson!

After reflecting, I think I did not manage our time appropriately.  A teacher new to Desmos might be overwhelmed with all the new information and not want to commit to diving into the site themselves with only 10 minutes left.  I also think I gave them too many options without enough structure.  In the future, I might ask that everyone find one activity to share in a google doc.  I could have the google doc separated by subjects as well.  We could walk through different challenges together and share as we go.

While there are things I will change in future sessions, I think overall the session went well and many teachers left excited about Desmos.

Please let me know of any suggestions you might have!

Here is the link to my presentation:  Creating a Student Centered Classroom Through Desmos

1st Day of School

For the last few years I have started the year by giving students a Sudoku puzzle when they come in the first day of school.  I explain the rules and let them work in small groups.  After they work a few minutes I stop them and pose the question “Is Sudoku math?”  I have them write down yes or no and some sort of justification.  I begin emphasizing that I am more concerned with the justification than the actual answer.  This emphasis is something that will continue throughout the year.

The distribution of answers varies greatly from class to class and year to year.  The discussion usually follows the same progression of key points though.

   Sudoku is math because it involves numbers.

   Sudoku is not math because there are no calculations.  You could use any 9 distinct symbols.

   Sudoku is math because it uses logic/problem solving/critical thinking.

I really enjoy leading students back and forth in this discussion.  There are some great thoughts into the structure of math (numbers, symbols, operations, logic,...). In the end, I try to leave the question open.  Many students feel uncomfortable without a clear answer.  I want them to start to become comfortable with uncertainty.  I want them to experience math in my class with an open mind and decide for themselves.  Based on their experiences with math so far, they may not think Sudoku is math.  Hopefully, I can provide them with new experiences this year so they don’t just think of math as numbers and calculations.

After exploring the MTBoS, I feel as though I need to provide my students with more explicit guidance for working collaboratively in groups.  I love this broken circles activity from Sarah Carter.  I’m hoping I can work this in without losing the opportunity to have a rich discussion on defining math on the first day.  Ideally, I would like to set the tone for the year by challenging students’ beliefs of math while also pushing students to work collaboratively.

I listed a few other activities I came across that I really like as well.

Henri Picciotto assigns for homework a short math autobiography with goals for math this year.

Jon Orr uses a “Math is like…” prompt.

I've used the Marshmallow Challenge at the end of the year after testing but it might be useful to start the year with it.